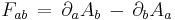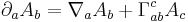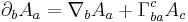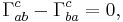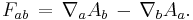Manifest covariance
In general relativity, an equation is said to be manifestly covariant if all expressions in the equation are tensors. The operations of addition, tensor multiplication, tensor contraction, raising and lowering indices, and covariant differentiation may appear in the equation. Forbidden terms include but are not restricted to partial derivatives. Tensor densities, especially integrands and variables of integration, may be allowed in manifestly covariant equations if they are clearly weighted by the appropriate power of the determinant of the metric.
Writing an equation in manifestly covariant form is useful because it guarantees general covariance upon quick inspection. If an equation is manifestly covariant, and if it reduces to a correct, corresponding equation in special relativity when evaluated instantaneously in a local inertial frame, then it is usually the correct generalization of the special relativistic equation in general relativity.
Example
An equation may be Lorentz covariant even if it is not manifestly covariant. Consider the electromagnetic field tensor
where 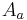 is the electromagnetic four-potential in the Lorenz gauge. The equation above contains partial derivatives and is therefore not manifestly covariant. Note that the partial derivatives may be written in terms of covariant derivatives and Christoffel symbols as
is the electromagnetic four-potential in the Lorenz gauge. The equation above contains partial derivatives and is therefore not manifestly covariant. Note that the partial derivatives may be written in terms of covariant derivatives and Christoffel symbols as
For a torsion-free metric assumed in general relativity, we may appeal to the symmetry of the Christoffel symbols
which allows the field tensor to be written in manifestly covariant form